Wat Is Een Gelijkbenige Driehoek? Alles Wat Je Moet Weten!

Wat is een gelijkbenige driehoek?

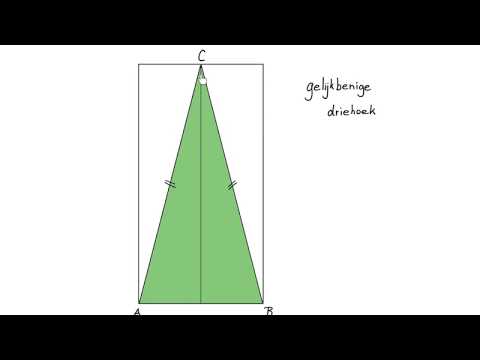
Een gelijkbenige driehoek is een driehoek waarvan twee zijden even lang zijn. Dit betekent dat de twee zijkanten die aan de basis van de driehoek zitten gelijk van lengte zijn en de derde zijde, de schuine zijde genaamd, kan een andere lengte hebben. In een gelijkbenige driehoek kunnen ook hoeken gelijk zijn.

Gelijkbenige driehoeken zijn een belangrijk onderwerp in de meetkunde en komen veel voor in verschillende toepassingen. Ze hebben unieke eigenschappen en formules die relevant zijn voor het berekenen van zijden en hoeken. In dit artikel zullen we dieper ingaan op wat een gelijkbenige driehoek is, de kenmerken ervan, de formules en eigenschappen, hoe je zijden en hoeken kunt berekenen en enkele toepassingen en voorbeelden van gelijkbenige driehoeken.

Kenmerken van een gelijkbenige driehoek

Gelijkbenige driehoeken hebben enkele specifieke kenmerken die ze onderscheiden van andere driehoeken:

1. Twee zijden zijn even lang: In een gelijkbenige driehoek zijn de lengtes van de twee zijden die aan de basis van de driehoek zitten gelijk. Deze zijden worden de benen genoemd. De derde zijde, de schuine zijde, kan een andere lengte hebben.

2. Gelijkheid van hoeken: In een gelijkbenige driehoek zijn de hoeken tegenover de gelijke zijden gelijk. Dit betekent dat de twee hoeken die tegenover de benen liggen gelijke waarden hebben.

3. Symmetrie: Een gelijkbenige driehoek heeft een symmetrieas. Deze as is de hoogtelijn die door de top van de driehoek en het midden van de basis gaat. De hoogtelijn verdeelt de driehoek in twee gelijke delen.

Formules en eigenschappen van een gelijkbenige driehoek

Gelijkbenige driehoeken hebben enkele belangrijke formules en eigenschappen die van toepassing zijn bij het berekenen van zijden en hoeken:

1. Zijden: De lengtes van de twee zijden die aan de basis van de driehoek zitten zijn gelijk. Deze lengte kan worden aangeduid als a. De lengte van de schuine zijde kan worden aangeduid als c.

2. Hoeken: De twee hoeken tegenover de gelijke zijden zijn gelijk en worden aangeduid als α. De hoek aan de top van de driehoek wordt aangeduid als β.

3. Hoekensom: De som van de hoeken in een gelijkbenige driehoek is altijd gelijk aan 180 graden. Dit betekent dat α + α + β = 180 graden.

4. Basis-hoek tussenstelling: De hoek tussen de twee gelijke zijden is gelijk aan de helft van de derde (top)hoek. Dit betekent dat α = β/2.

Hoe bereken je de zijden en hoeken van een gelijkbenige driehoek?

Het berekenen van de zijden en hoeken van een gelijkbenige driehoek kan op verschillende manieren worden gedaan, afhankelijk van de beschikbare informatie. Hier zijn enkele methoden:

1. Met gebruik van de hoekensom: Als je de waarde van één hoek kent, kun je de andere hoeken berekenen met behulp van de hoekensom van 180 graden. Met de bekende hoeken kun je vervolgens de lengte van de zijden berekenen met behulp van trigonometrische functies zoals sin, cos en tan.

2. Met behulp van de congruentie: Als je weet dat twee zijden gelijk zijn, kun je de lengte van de derde zijde berekenen met behulp van de congruentie van zijden. Je kunt ook de waarde van de hoeken berekenen met behulp van de formules en eigenschappen van een gelijkbenige driehoek.

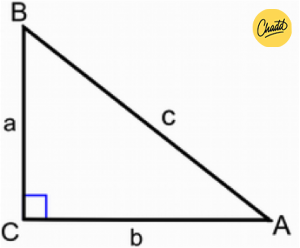
3. Met de Pythagoreïsche stelling: Als je weet dat de gelijke zijden rechthoekig zijn, kun je de lengte van de derde zijde berekenen met behulp van de Pythagoreïsche stelling. Je kunt ook de waarde van de hoeken berekenen met behulp van de eigenschappen van een rechthoekige driehoek.

Toepassingen en voorbeelden van gelijkbenige driehoeken

Gelijkbenige driehoeken worden veel gebruikt in verschillende toepassingen. Hier zijn enkele voorbeelden:

1. Architectuur: Gelijkbenige driehoeken worden gebruikt bij het ontwerpen en construeren van gebouwen, bruggen en andere structuren. Ze helpen bij het creëren van symmetrie en evenwicht in het ontwerp.

2. Driehoeksmeting: Gelijkbenige driehoeken worden gebruikt bij driehoeksmeting om hoogtes en afstanden te meten. Door het toepassen van trigonometrie op gelijkbenige driehoeken kan de lengte van onbekende zijden en de waarde van onbekende hoeken worden berekend.

3. Meetkunde: Gelijkbenige driehoeken bieden een basis voor het begrijpen van meer complexe meetkundige concepten, zoals congruentie, gelijkvormigheid en driehoeksconstructies.

Veelgemaakte fouten bij het werken met gelijkbenige driehoeken

Bij het werken met gelijkbenige driehoeken kunnen enkele veelgemaakte fouten voorkomen. Hier zijn enkele veelvoorkomende fouten:

1. Verwarring tussen gelijkzijdige en gelijkbenige driehoeken: Een gelijkzijdige driehoek is een speciaal type gelijkbenige driehoek waarin alle zijden even lang zijn. Het is belangrijk om het verschil tussen deze twee termen te begrijpen en correct te gebruiken.

2. Verkeerde toepassing van formules en eigenschappen: Het is essentieel om de juiste formules en eigenschappen van gelijkbenige driehoeken toe te passen om nauwkeurige berekeningen te krijgen. Het niet correct identificeren van de gegeven waarden kan leiden tot foutieve resultaten.

3. Geen rekening houden met de eenheid van meting: Bij het werken met zijden en hoeken is het belangrijk om consistent te zijn met de eenheid van meting. Het niet omrekenen van verschillende eenheden kan tot fouten leiden.

4. Onnauwkeurige metingen: Onnauwkeurige metingen kunnen leiden tot onnauwkeurige berekeningen. Het is belangrijk om zorgvuldig en nauwkeurig te meten bij het werken met gelijkbenige driehoeken.

De kennis van gelijkbenige driehoeken is essentieel in de meetkunde en andere vakgebieden waar geometrische concepten worden toegepast. Door de formules, eigenschappen en toepassingen van gelijkbenige driehoeken te begrijpen, kunnen we complexe berekeningen en constructies uitvoeren die nodig zijn in verschillende situaties.

Wat Betekent Een Gelijkbenige Driehoek?

Hoe Herken Je Een Gelijkbenige Driehoek?

Wat Betekent Gelijkzijdige Driehoeken?

Hoe Toon Je Aan Dat Een Driehoek Gelijkbenig Is?

Ontdekken 48 wat is een gelijkbenige driehoek